Many people are still mystified by PID, which stands for Proportional Integral Derivative. It is not, therefore, a great surprise that many are concerned about the thought of grappling with the complexities of feedback control.  Let us explain…

PID controller examines feedback, or ‘error’ signals from sensors placed in a process. When a feedback is received, it is compared with the desired or ‘set’ value and a calculation is made to match it to that set value.
Taking a typical application, such as an oven (see Figure 1), the measured temperature, referred to as the process value (PV), is fed into the controller and compared to the set value (SV) – the desired temperature.
As the temperature rises, power to the oven is reduced by the controller until the desired temperature is reached.

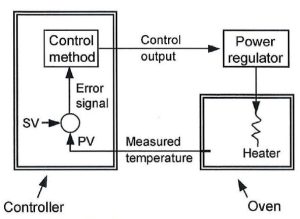
Figure 1: PID diagram of a typical industrial oven.

Most industrial processes require a very stable ‘straight-line’ control of temperature. The example shown assumes that the variable is temperature, but the principles are equally applicable to all analogue variables.
The ‘official’ PID explanation goes like this:

• P is the factor that determines the basic rate of change at the output in response to changes in the input.
• This proportional element is modified by the I, which is based on the time that a difference between set value and process-value exists.
• D is a function of the rate of change while the process value is moving with respect to the set value.

The integral function prevents the initial overshoot on power-up, while the derivative function eliminates the temperature instability over time once the set value is achieved and the process is under control.  Most heating applications can be handled by proportional control only. A proportional controller has the ability to vary its output between 0 and 100% and this enables it to continuously adjust the output so that the power input to the process is in balance with the process demand.
The range where the output power is adjusted is called the proportional band (PB).  The difference between the stabilised PV and SV is called ‘offset’ and can reduced by narrowing the proportional band. However the PB can only be reduced so far before instability occurs and this is where the Integral comes in.
Integral, also called ‘reset’, has the primary function of eliminating offset. This eliminates the temperature offset condition caused by proportional control on system start-up. To reduce or eliminate overshoot, we must use the derivative.

Thermal systems
In many thermal systems, overshoot (or undershoot) of the set value temperature is acceptable. However, in some systems this can produce poor quality products or damage equipment.
So derivative has one main job: to prevent or reduce overshoot and undershoot.  If the temperature rise is too fast, it will begin switching the heater off to prevent overshoot.  If the temperature is falling too fast, it will begin switching the heater on longer to prevent undershoot.
Another way to think of derivative is that it opposes change. For example, if the temperature rapidly drops below the SV, derivative opposes this by turning the heater on full.
Today, most PID controllers come with automatic PID tuning. However, if you ever feel brave enough to have a go yourself remember that increasing the PB will result in tighter control but will give a slower response, taking longer to reach the set value. A narrow PB generates a smaller offset than a wide PB. Too fast a reset (integral) causes overshoot while too slow a reset delays recovery. Finally, a long rate (derivative) time may cause overshoot, while a short rate time may cause a delay in recovery.

Our robust product range of Temperature Controllers and PID Process Controllers provide excellent control performance with a wide variety of functionality to suit all budgets.  You can view our Temperature Controllers here.

If you have any questions then please call us on 01323 811100 or use the Live Help on our website.